Jack Neubecker’s Homepage

About me

I am a PhD student of mathematics at the University of Queensland, studying resolvability and block-colouring of triple systems. In my honours thesis I studied Hamilton decompositions of infinite Cayley graphs, also at UQ. My research interests are primarily in combinatorics and discrete mathematics, in particular graph theory, design theory, and abstract algebra. I also enjoy problems in statistics, probability, and computer science, and I am always keen to collaborate with those in the sciences and arts to apply any of these topics.

Publications

Journal Articles

[1] Almost resolvable duplicated Steiner triple systems.
with Darryn Bryant and Sara Davies
Australasian Journal of Combinatorics 88(2) pp. 256-265, 2024.

pdf

Journal

Blog post

Recent work

In a paper published with Darryn Bryant and Sara Davies, we show that there exists a Steiner triple system of order $v$ having a set of almost parallel classes in which each triple occurs exactly twice if and only if $v \equiv 1 \pmod{6}$ and $v \notin \{7,13\}$ .

Here’s an example with $v = 19$ , and I also wrote a blog post explaining it.

Slightly less recent work

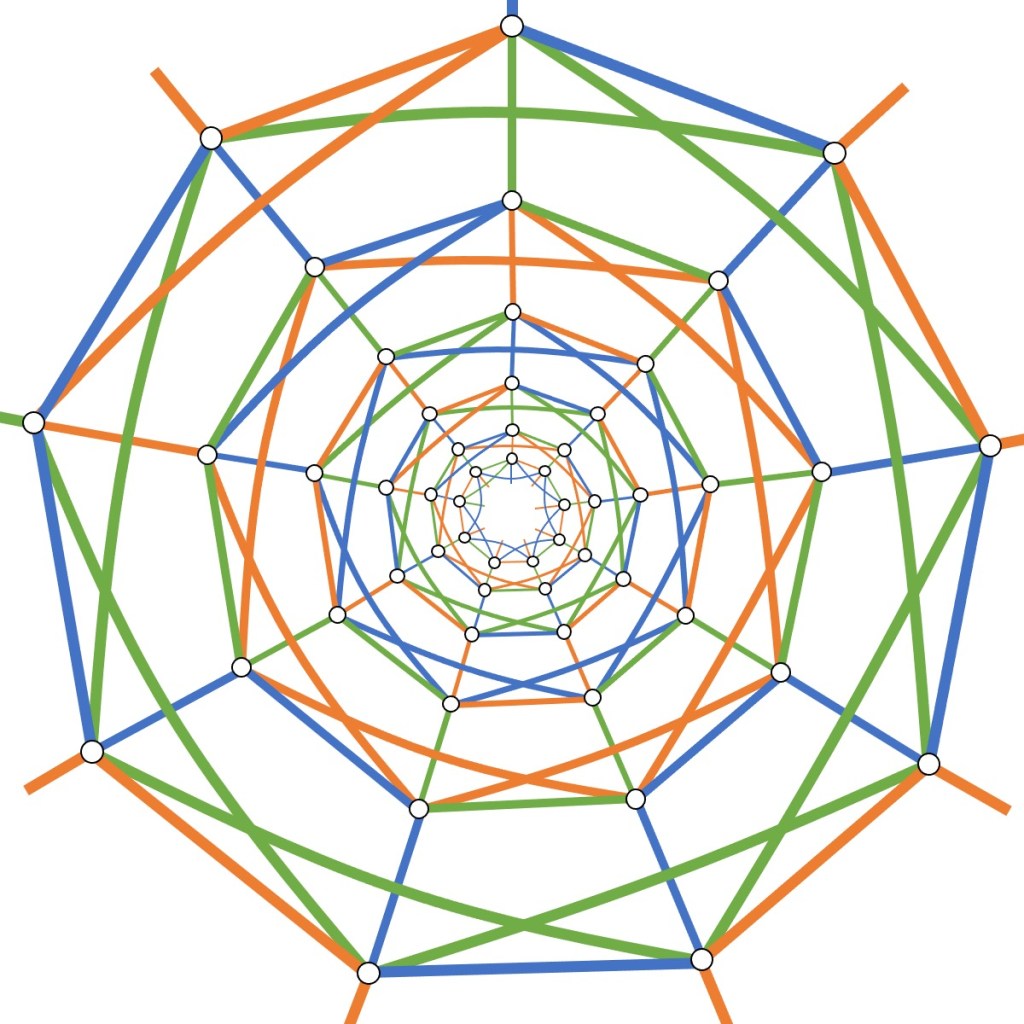
Can a multi-coloured family of spiders build a web like this without repeating themselves, and such that each coloured spider has a way of visiting any point on the web?

My honours research focused on how conjectures from finite graph theory can be generalised to infinite graphs. In particular, Cayley graphs and Cartesian products of graphs have structures which are conducive to Hamilton decompositions in both finite and infinite contexts, and a lot of finite results can be extended to infinite graphs.

SSC 2022

Together with some other wonderful combinatorics students, we organised the student symposium in combinatorics in May-June 2022. Students at all stages of their studies were invited to attend this online symposium, and we were proud to host eleven excellent plenary talks, all from current students in combinatorics and its applications.

Problems I would like to see solved

For every pair of integers $a$ and $b$ , does there exist an integer which is a multi-digit palindrome in both base $a$ and $b$ ?

Computational evidence suggests so, and I can construct certain infinite families of examples, but the general problem seems to be beyond my number theory skills. More details available here.

Does this graph have a Hamilton decomposition? Many other similar graphs do, say if we replace the triangles with single points, squares, or other even-sided polygons. But we don’t have a easily constructible picture of those even-sided cases to suggest a similar structure in this graph, or others built from odd-sided polygons. The inefficiency of constructing and visualising these graphs is a large obstacle to progress. More details available here.

Other things about me

I also like things other than maths, believe it or not. Take a look around and you might notice I also like sports (handball, basketball, cricket and soccer amongst others), photography, linguistics, comedy, and various other goof-offs. These aren’t always interesting enough to write about, but it’s nice to know these sorts of things about a person. I have taken a leaf out of Phil Pollett’s book and written out a list if you’re interested.

You might even find my CV somewhere on here, or how to contact me if you’re interested in collaborating on research, creative works, teaching, or just want to have a chat. If you’d like to read the work published here in a good old-fashioned blog format, click the blog posts button up the top. Some of these posts date back to high school, so the techniques might look a little rudimentary by my current standards, but I’m nonetheless pleased with the work and the picture it paints of my academic journey.